I have always been fascinated in unsolved mathematics problems, since we had recently talked about Carl Friedrich Gauss I thought it would be fitting to make this blog post about The Gauss Circle Problem. The interesting thing about The Gauss Circle Problem is that is appears to be a simple counting problem but is actually a pretty complex problem. The Gauss Circle Problem is to count the number of lattice points inside the boundary of a circle with radius r with the center at the origin. Basically we are considering a circle in R2 with center at the origin and radius >= 0, the circle problem is asking how many points can fit into the circle in the form (m,n) where m and n are integers. We know the equation of the circle can be represented by x2 + y2 = r2 so we are just really looking for the number of pairs of integers m,n that satisfy the equation m2 + n2 <= r2.
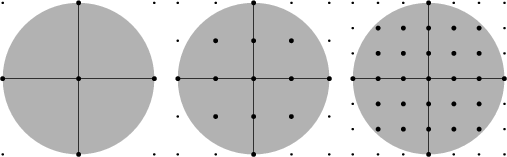

The area of a circle with radius r is given by πr2, and since a square with area one contains one integer point are number of lattice points N(r) can be expected to be roughly πr2 but it is not exactly quite that so we have some error term E(r). Which is how Gauss got the equation
 .
.
Now the issue was figuring out the error term of N(r), It has been proven that N(4) = 49, N(sqrt(17)) = 57, N(sqrt(18)) = 61 notice that r does not have to be an integer but that our error term varies depending on our r. So the next step was to find a lower and upper bound for E(r) so that we can narrow down our value of N(r). Gauss was able to prove that the upper bound of E(r) is

(Graphical Representation of Proof)
Unfortunately I could not find Gauss's proof of solving the upper bound of E(r). Gauss was unable to figure out the lower bound of E(r). Mathematicians decades later were able to figure out the lower bound of E(r), Hardy and Landau independently both figured out the lower bound. They figured out the lower bound by both showing

they both came to the conclusion that by writing E(r) as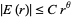 the lower bound is 1/2. Since they rewrote E(r) as
the lower bound is 1/2. Since they rewrote E(r) as 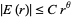 improvements has been made with finding the upper bound
improvements has been made with finding the upper bound
This table curiosity of wolfram shows the incremental increase in finding the upper bound. Even though both bounds have been found I believe the Gauss Circle Problem is still unsolved, Sylvain E. Cappell and Julius L. Shaneson have been working on solving the problem but last I know of their paper is still under revision because of some errors in their proof. The Gauss Circle problem seems like an easy enough problem at first glance but it is actually a very complicated problem. In this blog post I barely even touched on how complicated and dense the work on The Gauss Circle is.
 .
.Now the issue was figuring out the error term of N(r), It has been proven that N(4) = 49, N(sqrt(17)) = 57, N(sqrt(18)) = 61 notice that r does not have to be an integer but that our error term varies depending on our r. So the next step was to find a lower and upper bound for E(r) so that we can narrow down our value of N(r). Gauss was able to prove that the upper bound of E(r) is

(Graphical Representation of Proof)
Unfortunately I could not find Gauss's proof of solving the upper bound of E(r). Gauss was unable to figure out the lower bound of E(r). Mathematicians decades later were able to figure out the lower bound of E(r), Hardy and Landau independently both figured out the lower bound. They figured out the lower bound by both showing

they both came to the conclusion that by writing E(r) as
| approx. | citation | |
| 1 | 1.00000 | Dirichlet |
| 2/3 | 0.66667 | Voronoi (1903), Sierpiński (1906), van der Corput (1923) |
| 37/56 | 0.66071 | Littlewood and Walfisz (1925) |
| 33/50 | 0.66000 | van der Corput (1922) |
| 27/41 | 0.65854 | van der Corput (1928) |
| 15/23 | 0.65217 | |
| 24/37 | 0.64865 | Chen (1963), Kolesnik (1969) |
| 35/54 | 0.64815 | Kolesnik (1982) |
| 278/429 | 0.64802 | Kolesnik |
| 34/53 | 0.64151 | Vinogradov (1935) |
| 7/11 | 0.63636 | Iwaniec and Mozzochi (1988) |
| 46/73 | 0.63014 | Huxley (1993) |
| 131/208 | 0.62981 | Huxley (2003) |
Interesting problem to highlight. There's a whole class of problems like this, where mathematicians just try to improve on an estimate. You get these tiny advances and then a huge jump.
ReplyDeleteNice post! 5Cs +